The actual science of logic is conversant at present only with things either certain, impossible, or entirely doubtful, none of which (fortunately) we have to reason on. Therefore the true logic for this world is the calculus of Probabilities.

JAMES CLERK MAXWELL

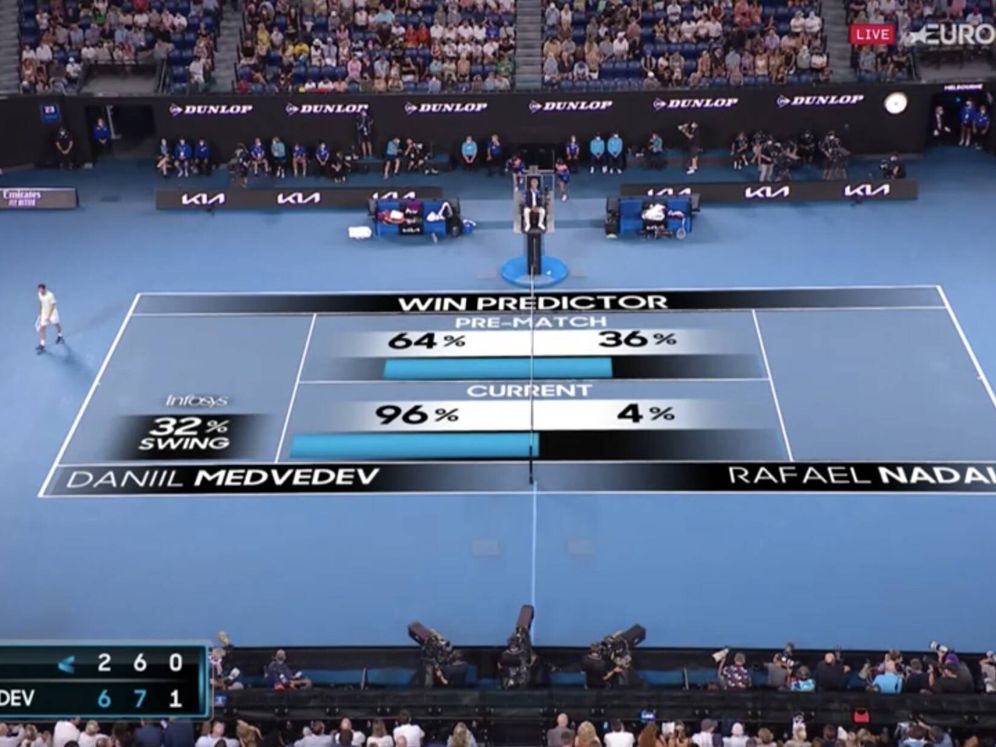
El 30 de enero de 2022 Rafa Nadal protagonizó una de las victorias más épicas de su carrera profesional. El manacorí remontó  al ruso Medvédev en una final agónica del Open de Australia. Tan mal estaban las cosas, que tras perder el segundo set, la inteligencia artificial de la ATP pronosticaba que Nadal tenía sólo un 4 % de probabilidad de ganar¹.

Pero, ¿qué significa que tuviera un 4 % de probabilidad de ganar?. Esta pregunta plantea interrogantes que apuntan a la noción misma de probabilidad. Esta definición sigue hoy en día generando un debate acalorado entre dos visiones dentro de la estadística.

Dos interpretaciones: frecuentista vs. bayesiana 

Por un lado, tenemos la interpretación frecuentista. Antes de entrar de lleno en esta interpretación vamos a partir de una versión simplificada, denominada interpretación clásica. Esta primera versión define la probabilidad como el cociente entre casos favorables frente a casos posibles. Esta definición de probabilidad permite responder a preguntas cómo ¿cuál es la probabilidad de obtener un 5 o un 6 al lanzar un dado? La respuesta es fácil, número de casos favorables: 2, que salga un 5 o un 6; número de casos posibles: 6, uno por cada cara del dado. La probabilidad de este evento es 1 ⁄ 3, o aproximadamente, un 33 %. Si intentamos traducir esta interpretación el 4 % de probabilidad que tenía Rafa Nadal se nos presentan serias dificultades, ya que tenemos que convertir este 4 % en una fracción ¿a qué cociente corresponde: 4 / 100, 40 / 1000, 400 / 10000…? Hay infinitos cocientes que dan como resultado ese 4 %.

Para seguir avanzando podemos recurrir, ahora sí, a la interpretación frecuentista. Esta considera que la probabilidad es el número al que se aproxima el cociente anterior cuando se repite un experimento un número infinito de veces. En el caso del dado, la probabilidad sería el límite al que se aproxima el cociente entre casos favorables y posibles cuando se tira el dado un número infinito de veces. El resultado de este límite sigue siendo 1 / 3. Trasladándolo a nuestro ejemplo, si Rafa y Medvédev hubieran jugado un número infinito de partidos partiendo de ese segundo set, entonces el 4 % se corresponde al porcentaje de partidos que hubiera ganado Rafa. Intuitivamente podemos llegar a imaginar que esta interpretación está cuantificando la proporción de universos paralelos en los que Nadal gana el partido. En cada uno de estos universos se desarrolla un partido distinto debido a modificaciones al azar en las diversas condiciones del juego y las posibles respuestas de los jugadores. Tras infinitos partidos el cociente entre partidos ganados por Nadal, y partidos jugados terminaría convergiendo al 4 %.

Esta interpretación se la considera objetiva ya que solo existe una única probabilidad que se le asocia a la victoria de Nadal. Objetivamente inútil en este caso, ya que no hay inteligencia artificial o natural capaz de simular tal cantidad de escenarios. Ni siquiera un número finito de los mismos. La interpretación frecuentista funciona bien cuando trabajamos con monedas, dados o situaciones donde podemos repetir un mismo experimento múltiples veces pero hace aguas cuando hablamos de eventos únicos o muy infrecuentes.

Por otro lado, tenemos la interpretación bayesiana que considera la probabilidad como el resultado de formalizar numéricamente una creencia. Dado un enunciado, como por ejemplo, «Rafa Nadal ganará el partido», la probabilidad mide el grado de certeza de que sea verdadero.  En este sentido, la probabilidad que nos presenta la imagen expresa la opinión que tiene la inteligencia artificial sobre las posibilidades que Rafa tiene de ganar el partido en ese preciso instante del torneo.

Este grado de certeza es subjetivo ya que distintos observadores pueden asignar distintas probabilidades al mismo enunciado. De hecho, si se hubiera preguntado a cada espectador cuál era el grado de confianza, expresado en términos probabilísticos, de que Nadal iba a ganar en ese momento del partido, se hubieran obtenido un gran variedad de probabilidades siendo la gran mayoría menores incluso que el 4 % que pronosticaba la inteligencia artificial.

¿Quién tiene razón?

Si pueden existir tantas respuestas como observadores (humanos o artificiales), entonces, ¿cómo sabemos cuál de ellos da la respuesta correcta? Tenemos que salvar dos obstáculos para responder a esta pregunta.

En primer lugar, si nos ponemos estrictos es imposible determinar si el modelo acertó o falló en el pronóstico. Cualquier probabilidad distinta de cero contempla la posibilidad de que Rafa Nadal gané el encuentro por minúscula que sea. Un escenario con una probabilidad del 1 % incluye la posibilidad que Rafa gane el partido. Expresa muy poca confianza en que este evento ocurra pero no lo descarta por completo. Solo con una probabilidad igual a cero estaríamos afirmando que estamos seguros de que ese evento no se va a producir.

En segundo lugar, las predicciones del modelo cambian a medida que avanza el partido. La estimación en el segundo set era del 4 %. Esta estimación va a aumentando a medida que evoluciona el partido favorablemente para Nadal. Si el modelo recibe nueva información ajusta sus predicciones en consonancia. Lo mismo hacen los observadores humanos. A no ser que esté mal diseñado el modelo, o que preguntemos a un fanático,  nuevas evidencias deberian modificar el pronóstico sobre quien va a ganar el partido. Por descontado que cada observador puede reaccionar distintos ante la misma evidencia, de manera que el impacto en sus nuevas estimaciones no tiene porque ser el mismo.

Teniendo en consideración lo anterior, lo más prudente sería abstenerse de valorar la calidad del modelo de la ATP. Poco se puede decir de un modelo del que solo conocemos un pronóstico. Un buen punto de partida para realizar una evaluación del modelo sería disponer de todas las predicciones que realizó durante el partido para poder cotejar con la evolución del tanteo. Una evaluación más robusta requiere ampliar esta comparación a diversos momentos que se produzcan en múltiples partidos. La selección de estos momentos tiene que ser lo suficientemente variada para que constituyan una muestra lo más representativa de partidos profesionales de tenis. Idealmente tendría que incluir partidos con diferentes jugadores en momentos con distintas combinaciones de puntuaciones en el marcador. Como nos indica Nate Silver² un buen modelo es aquel que realiza pronósticos coherentes a lo largo de toda la evaluación. Cuando dice que uno de los jugadores tiene un 4 % de ganar esto ocurre un 4 % de las veces, cuando predice que gana un 50 %, ocurre un 50 %, y si predice una victoria con un 96 %, ésta ocurre el 96 %.

Este proceso de validación del modelo se le denomina calibración. Cuando un modelo está bien calibrado es útil para tomar decisiones. Por ejemplo, si tenemos un modelo bien calibrado que predice que hay un 40 % posibilidades que empiece una guerra deberíamos preocuparnos mucho, si sube a un 60 % puede ser momento de salir del país³.

En cambio si un modelo está mal calibrado la toma de decisiones puede llegar a ser desastrosa. El propio Nate Silver nos da uno de los ejemplos de modelo mal calibrado que ha tenido más impacto. Durante la crisis financiera de 2008 las agencias de rating determinaron que las CDO (Collateralized Debt Obligation) tenían un probabilidad de 0.12 % de impago en los siguientes cinco años después de su adquisición. Este instrumento financiero mezclaba hipotecas con riesgo muy variado incluyendo las hipotecas basura (en inglés, subprime). Los análisis posteriores a la crisis demostraron que el 28 % de estos terminaron en impago ―en las estimaciones más conservadoras―, lo cual supone 200 veces más alto que lo que habían predicho las agencias de rating.

Probabilidad a priori

Hay una diferencia más sustantiva entre las dos aproximaciones que ahora sólo la podemos esbozar. Los defensores de la estadística frecuentista sostienen que para determinar la probabilidad se calcula únicamente teniendo en cuenta las evidencias que aportan los datos, mientras que en la estadística bayesiana se integran los datos con las creencias que a priori se tuvieran. Esto suena un tanto abstracto así que volvamos al ejemplo. Si nos fijamos en la imagen además de la probabilidad de ganar en ese instante (4 %) también aparece la probabilidad que tenía Rafa de ganar antes de empezar el partido (36 %). Vamos a suponer que ese 4 % ha sido calculado empleando únicamente datos recopilados durante el partido (dos jugadores anónimos) sin tener en cuenta quienes información antes previa al partido. Por el contrario, ese 36 % resume la confianza sobre las probabilidades de ganar de Nadal antes de jugar. Esta probabilidad a priori incluye la percepción sobre el estado físico de Nadal, la confianza en su desempeño en una final, la motivación para el partido, los enfrentamientos previos entre los dos jugadores… La metodología frecuentista únicamente emplea los datos recopilados durante el partido (4 %) mientras que la bayesiana proporciona un método universal para integrar el conocimiento a priori con los datos generando una nueva probabilidad a posteriori que actualiza la creencia en las posibilidades.

Lo mejor de dos mundos

Aunque estas dos interpretaciones se han presentado históricamente  como antagónicas realmente se complementan bastante bien. Desde un punto de vista práctico, el cálculo de una probabilidad como una proporción de casos favorables frente a casos posibles se puede aplicar en infinidad de ocasiones. En el caso del partido de Nadal podríamos emplear datos de otros partidos históricos en el que se haya llegado a una situación similar en el segundo set, y calcular la proporción en los que el jugador que iba por detrás en el marcador terminó ganando el partido. No se corresponde completamente con la interpretación ortodoxa de la visión frecuentista que hemos planteado pero puede ser una buena aproximación.

La interpretación bayesiana es inevitable aunque calculemos las probabilidades como proporciones siguiendo la lógica frecuentista. Por una lado, en problemas reales cualquier modelo que empleemos para calcular una probabilidad siempre va a ser una aproximación a la realidad que se basa en serie de asunciones, que están la mayoría de la veces implícitas, que condicionan el resultado. Distintos modelos con distintas asunciones van a tener inevitablemente resultados distintos. Entender las probabilidades como creencias sobre el grado de certidumbre nos posiciona en una situación más realista que nos obliga a tener presente en cada situación cuáles son los presupuestos que se han asumido en la construcción del modelo.

En esta línea la aproximación bayesiana incorpora una distinción fundamental entre el grado de confianza antes de conocer los datos (probabilidad a priori) y después de conocer los datos (probabilidad a posteriori). Esto permite explicar cómo ante la misma situación dos observadores que hayan tenido acceso a los mismos datos puedan llegar a conclusiones distintas sobre la plausibilidad de un enunciado. Volviendo una vez más al ejemplo, supongamos que el partido ha sido amañado. El resultado final ha sido pactado entre Nadal, Medvédev y un corredor de apuestas. Para aumentar lo máximo posible las ganancias, los dos jugadores han estado simulando que Medvédev va a arrasar a Nadal. Si en el segundo set se pregunta a una espectador al azar dirá que las posibilidades de ganar de Nadal son muy bajas, más bajas incluso que las que pronostica el modelo, a tenor de cómo están jugando. En cambio, si se pregunta al corredor de apuesta dirá que las posibilidades de ganar de Nadal estarán cerca del 100 % (siempre cabe la posibilidad de que alguno de los jugadores se arrepienta y rompa el trato). Lo que ocurra en la pista apenas afecta a las creencias del corredor de apuestas que se mantienen muy parecidas a las que tenía antes de empezar el partido. Las dos personas están viendo el mismo partido, esto es, reciben los mismos datos, pero las probabilidades a priori afectan distinto a cada uno. Mientras que el corredor de apuestas básicamente se fia de sus creencias a priori e ignora los datos, el espectador se deja llevar principalmente por lo que está ocurriendo en la pista. Esta distinción nos lleva a una máxima que habría que tatuarse en el cerebro, cuanta más información veraz se dispone, mayor precisión debería tener el modelo. Así, dos modelos que tienen acceso a diferente información darán a la fuerza distintas probabilidades para el mismo evento. 

En resumen

Probabilidad es el lenguaje que utilizamos para poder formalizar razonamientos que están sujetos a la incertidumbre. Se puede ver como una extensión del razonamiento lógico-deductivo. En lógica una proposición («Nadal ganará el partido») puede ser verdadera o falsa, En probabilidad tenemos un rango de posibilidades que se expresa el grado de confianza de que una proposición sea verdadera. Este rango varía desde 0 (totalmente seguros que es falsa) a 100 % (totalmente seguro que es verdadera). Es común en probabilidad hablar de eventos en vez de proposiciones, esto es, cuál es la probabilidad de que ocurra un determinado evento.  Hay que tener en cuenta que cuando no disponemos de ninguna información ni tenemos ningún criterio en el que basarnos tenemos que asignar una probabilidad del 50 %. Sería el equivalente a lanzar una moneda al aire. Cualquier otra probabilidad distinta del 50 % refleja que tenemos una inclinación, por mínima que sea, hacia que ocurra o no el evento. El razonamiento probabilístico extiende el razonamiento lógico para incorporar la falta de información.

La interpretación frecuentista aporta  una manera sencilla e intuitiva de estimar la probabilidad de un evento, siempre que se pueda conceptualizar con un experimento repetible en el tiempo. Los métodos estadísticos derivados de esta interpretación son la opción mayoritaria en la práctica profesional, y son los que se explican por defecto en los manuales de estadística.  Por su parte, la interpretación bayesiana es más genérica. Esta interpretación es independiente de cómo se calculen esas probabilidades. Sus detractores le achacan falta de objetividad. Aunque, hemos visto que la objetividad no es más que una ilusión. En realidad, nuestros razonamientos incorporan datos y creencias. Ignorar el conocimiento a priori para calcular la probabilidad de un evento puede llevar a conclusiones absurdas como hemos visto. Esto ocurre tanto en razonamientos de la vida cotidiana como en la práctica científica. Por su parte, los defensores de la estadística bayesiana consideran que los métodos de la estadística frecuentista son simple e irremediablemente incorrectos⁴. Sin entrar en el debate, sí que es evidente que la interpretación bayesiana es más flexible que la frecuentista. Hemos visto que tiene dos ventajas principalmente. Primero, refleja mejor situaciones con múltiples observadores. Segundo, permite combinar evidencias empíricas (datos) con la información previa que tuviera el modelo, mientras que la interpretación frecuentista se limita únicamente a los datos. De todas formas, ambas interpretaciones conviven, en cierta medida, dentro del uso en el día a día de la estadística, y pueden llegar a ser complementarias en la práctica. Por ejemplo, emplear la proporción de eventos similares del pasado (frecuentista) como aproximación al grado de confianza (bayesiano) de que ocurra un evento da buenos resultados.

Notas

1. Esta noticia del Confidencial resaltaba que la inteligencia artificial no supo predecir la victoria de Nadal. En este artículo argumentaremos que el titular del Confidencial no es correcto, mientras que el pie de foto si que se acercaba más a la realidad: «La predicción de la ATP dejaba a Nadal con muy pocas opciones. (Eurosport)».
   https://www.elconfidencial.com/tecnologia/2022-01-31/nadal-inteligencia-artificial-open-australia-grand-slam_3367467/ ↩︎
2.  Nate Silver (2012). The Signal and the Noise. ↩︎
3. Este artículo de Kiko Llanera resume bien la importancia y necesidad del calibrar los modelos mediante ejemplos extraídos de plataformas online donde los usuarios realizan predicciones sobre todo tipo de eventos, como la guerra de Ucrania. https://elpais.com/tecnologia/2022-03-24/se-puede-predecir-el-futuro-de-la-guerra-en-ucrania-es-lo-que-intenta-una-comunidad-de-pronosticadores-en-internet.html ↩︎
4. Aubrey Clayton (2021) Bernoulli’s Fallacy: Statistical Illogic and the Crisis of Modern Science. 1st Edition. ↩︎